Explain Even and Odd Numbers

What are Even Numbers?

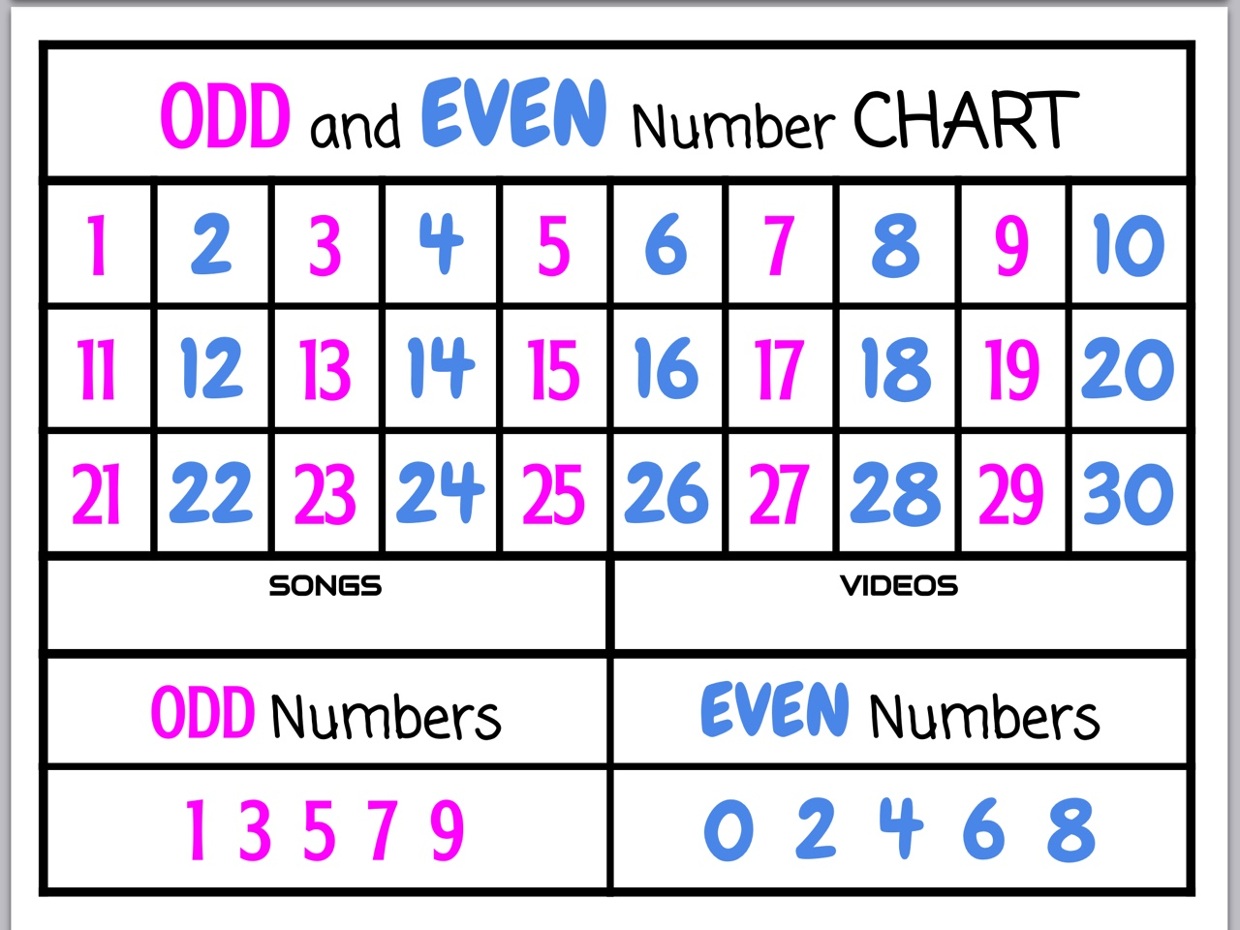
Even Numbers are integers that are perfectly and only divisible by 2, while odd numbers cannot be exactly divided by 2. The examples of even numbers are 4, 6, 10, 20, 40, etc. Numbers that always end up with their last digit as 0, 2, 4, 6, or 8 are called even numbers. A few examples of even numbers are 2, 88, 6, 8, 10, 12, 14, 16. These are called even numbers because these numbers can easily be divided by the table of 2. The smallest positive even natural number is 2.

How to Know If a Specific Number is Even or Odd?

To find out whether a particular number is odd or even, one needs to check the number in the unit’s place. That given number in the unit’s place will tell you whether the number is even or odd.

• Even Numbers perpetually end with 0, 2, 4, 6, 8
• Odd Numbers perpetually end with 1, 3, 5, 7, 9

Think about the numbers 3, 835, 517, which ends with an odd number that is 3, 5, and 7. Therefore, the given numbers 3, 845, 917 are odd numbers, and thus these particular numbers are not even numbers. In the same way, 8, 362 are even numbers as they end with 8 and 2.

Properties of Even Numbers

Three vital properties of even numbers are stated below:

1. The property of addition

Adding even and odd numbers or vice-versa, the resulting number will always be odd.

Example: 8 + 9 = 17,

5 + 16 = 21

Adding two even numbers, the resulting number will always be even.

Example: 12+10 = 22

Adding Two odd numbers, the resulting number will always be even.

Example: 15 + 9 = 24

1. The property of subtraction

Subtracting even numbers from odd or vice-versa, the resulting number will always be odd.

Example: 9 – 4 = 5

10 – 9 = 1

Subtracting even numbers from even, the resulting number will always be even.

Example: 16 – 6 = 10

Subtracting odd from odd, the resulting number will always be even.

Example: 21 – 9 = 12

1. The property of multiplication

Multiplying even and even numbers will always result in an even number.

Example: 6 × 2 = 12

12 × 4 = 48

Multiplying even and odd numbers will always result in an even number.

Example: 4 × 3 = 12,

6 × 3 = 18

Multiplying odd and odd numbers will always result in an odd number.

Example: 3 × 3 = 9,

5 × 3 = 15

What are Odd Numbers?

Odd numbers are the numbers that cannot be divisible by the number 2. It cannot be divided into two equal separate integers. If we divide an odd number by 2, then it will leave a remaining number. The examples are 1, 3, 5, 15, etc. Even numbers, unlike the odd numbers, are divided by the number 2, such as 2,4,24,8,20, etc. So, if n is an even number, then n+1 can be written to show an odd number. Odd numbers are stated as any number which is not divisible by two.

Fun Facts

• An odd number is an integer that is not divisible by the number 2
• If these numbers are divided by 2, then there will always be a remainder left.
• In the number line, number one is the first positive odd number.

Conclusion

Odd and Even numbers are the basis of mathematics. They build a solid base for your mathematical knowledge and will be helpful in your day-to-day activities as well. Odd and Even numbers will help students enhance their logical thinking and reasoning skills. You can understand the concept of even numbers and odd numbers with Cuemath. Cuemath is an online learning educational platform that engages students in the most interesting way through visual simulations, worksheets, puzzles etc.